Inductanță de scurgere derivă din proprietatea electrică a unui transformator conectat imperfect, în care fiecare înfășurare se comportă ca o autoinducție în ordine cu rezistență ohmică constantă a înfășurării. Aceste patru constante de înfășurare interacționează și cu inductanța reciprocă a transformatorului. Inductanța scurgerii înfășurării se datorează curentului de curgere, care nu se conectează la toate spirasele fiecărei înfășurări conectate imperfect.
Reactivitatea la scurgere este de obicei cel mai important element al unui transformator de sistem de putere datorită factorului de putere, căderii de tensiune, consumului de energie reactivă și considerațiilor de curent de defect. [1] [2]
Inductanța de scurgere depinde de geometria miezului și a înfășurărilor. Reducerea tensiunii în reactivitatea la scurgere duce la reglarea deseori nedorită a alimentării cu sarcină variabilă a transformatorului. Dar poate fi util și pentru izolarea armonică (atenuarea la frecvențe mai mari) a unor sarcini. [3]
Inducerea scurgerilor se aplică oricărui dispozitiv cu un circuit magnetic cu o conexiune imperfectă, inclusiv motoare. [4]
Cuplare inductivă și inductivă [editați]
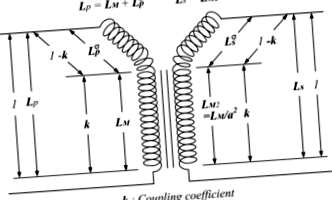
Fluxul circuitului magnetic, care nu conectează cele două înfășurări, este un flux de scurgere corespunzător inductanței de scurgere primare L P σ și inductanței de scurgere secundare L S σ. Referindu-ne la FIG. 1, acești inductori de scurgere sunt definiți cu privire la inductoarele cu circuit deschis ale unei înfășurări ale transformatorului și un factor de cuplare conectat sau factor de cuplare, [5] [6] [7]
Autoinducția de bază a circuitului deschis este dată de
^> este inductanța primară a scurgerii
este un factor de cuplare inductiv
Măsurarea principalelor inductoare ale transformatorului și a coeficientului de conectare
într-o conexiune suplimentară,
într-o scădere,
astfel încât aceste inductanțe ale transformatorului să poată fi determinate de următoarele trei ecuații: [9] [10]
Coeficientul de cuplare se obține din valoarea inductanței măsurată printr-o înfășurare cu cealaltă înfășurare, un scurtcircuit în conformitate cu următoarele: [11] [12] [13]
Pe echiv. 2.7,
Circuitul podului Campbell poate fi, de asemenea, utilizat pentru a determina auto-inductanța transformatorului și inductanța reciprocă utilizând o pereche dublă cu inductori standard variabili pentru o parte a podului. [14] [15]
Rezultă, prin urmare, că autoinductivitatea circuitului deschis și coeficientul de cuplare inductivă sunt date de
este inductanță reciprocă
^> este inductanța secundară a scurgerii
= L_/a ^> este inductanța de magnetizare referitoare la secundar
este un factor de cuplare inductiv
Validitatea electrică a circuitului transformatorului din fig. 1 depinde strict de condițiile circuitului deschis pentru inductorii considerați ai înfășurărilor. Condițiile mai generale ale circuitului sunt dezvoltate în următoarele două secțiuni.
Rată de scurgere inductivă și inductanță [editați]
Un transformator liniar non-ideal cu două înfășurări poate fi reprezentat de două circuite inductive interconectate care conectează cele cinci constante de impedanță ale transformatorului, așa cum se arată în FIG.
M este inductanța reciprocă
> &> sunt rezistențele primare și secundare ale înfășurărilor
Factorul de cuplare este definit ca
Coeficientul de rotație al înfășurării este: în practică este dat ca
/L_ >> = N_
/ N_ aproximativ v_
/ v_ aproximativ i_/i_ < P>=> ------ (Lv.2 2.2) . [19]
N P&N S sunt viraje primare și secundare
v P & v S și i P & i S sunt tensiuni și curenți de înfășurare primari și secundari.
Ecuațiile rețelelor de transformatoare non-ideale pot fi exprimate prin următoarele ecuații pentru tensiune și conexiune între flux, [20]
Câini _
= L_
cdot i_
-M cdot i_> ------ (nivel 2.5)
Câini _ = L_ cdot i_ -M cdot i_
> ------ (nivel 2.6),
>> este un derivat al conexiunii de streaming în raport cu timpul.
Aceste ecuații pot fi dezvoltate pentru a arăta că ignorarea rezistențelor de înfășurare asociate, raportul dintre inductanțe și curenți ai circuitului de înfășurare la celelalte înfășurări de scurtcircuit și în testul de circuit deschis este după cum urmează, [21]
i oc & i sc sunt circuite deschise și curenți de scurtcircuit
L oc & L sc sunt deschise și scurtcircuitate.
^> & ^> sunt scurgeri inductive de scurtcircuit primar și secundar.
Inductanța transformatorului poate fi caracterizată în raport cu cele trei constante de inductanță după cum urmează, [25] [26]
c este inductanța de magnetizare corespunzătoare reactivității de magnetizare X M
L P σ și L S σ sunt inductori de scurgere primari și secundari corespunzători scurgerilor reactive primare și secundare X P σ & X S σ .
Transformatorul poate fi exprimat mai convenabil ca circuit echivalent din FIG. 3 cu constante secundare indicate (adică, cu o inscripție primară) primare, [25] [26]
care permite exprimarea circuitului echivalent din FIG. 4 în termeni de înfășurări de scurgere și constante de inductanță de magnetizare, după cum urmează, [26]
Transformatorul non-ideal din FIG. 4 poate fi prezentat ca un circuit echivalent simplificat din FIG. 5, cu constante secundare referitoare la primar și fără izolarea ideală a transformatorului, unde,
> este curentul de magnetizare excitat de un curent care M, care conectează cele două înfășurări primare și secundare
'> este curentul secundar referitor la partea primară a transformatorului.
Rată de scurgere rafinată [editați]
Derivarea rafinată a coeficientului de scurgere inductivă
A. Pe echiv. 2.1 & IEC IEV 131-12-41 coeficientul de cuplare inductivă este dat de
b. Pe echiv. 2.7 & IEC IEV 131-12-42 Coeficient de scurgere inductiv < showstyle се дава от
sigma = 1-k ^ = 1 -> L_ >>> ------ (nivel 2.7) & (nivelul 3.7a)
Toate ecuațiile din această lucrare presupun condiții de frecvență constante (frecvență constantă). & < стойностите на които са безразмерни, фиксирани, крайни и положителни, но по-малки от 1.
Referindu-ne la diagrama de flux din FIG. 6, sunt utilizate următoarele ecuații: [28] [29]
σ P = P σ/Φ M = L P σ/L M [32] ------ (ur. Eq. 2.7)
= P = + M + Φ P σ = Φ M + σ P = M = (1 + σ P) [M [34] [35] ------ (nivelul 3.3)
'S' = Φ M + S σ '= Φ M + σ S = M = (1 + σ S) [M [36] [37] ------ (nivel 3.4)
L P = L M + L P σ = L M + σ P L M = (1 + σ P) L M [38] ------ (ecuația 3.5) Eq. 1.1b și echiv. 2.14)
L S '= L M + L S σ' = L M + σ S L M = (1 + σ S) L M [39] ------ (ecuația 3.6) Eq. 1.1b și echiv. 2.14),
σ P & σ S sunt factorul primar de scurgere și respectiv factorul secundar de scurgere
& M & L M sunt respectiv fluxul reciproc și inductanța magnetizării
P σ și L P σ sunt, respectiv, debitul primar de scurgere și inductanța primară de scurgere
S σ 'și L S σ' sunt debitul secundar de scurgere și respectiv inductanța de scurgere secundară, care se referă la fluxul primar.
Prin urmare, raportul de scurgere σ poate fi rafinat în ceea ce privește relația dintre inducția de inducție specifică și ecuațiile ecuației coeficientului de scurgere, după cum urmează: [40]
Aplicații [editați]
Inductanța de scurgere poate fi o proprietate nedorită, deoarece provoacă o schimbare a tensiunii cu sarcina.
În multe cazuri, acest lucru este util. Inductanța de scurgere are efectul benefic al limitării fluxurilor de curent într-un transformator (și sarcină) fără puterea disipantă (cu excepția pierderilor obișnuite ne-ideale ale transformatorului). Transformatoarele sunt de obicei proiectate să aibă o valoare specifică a inductanței de scurgere, astfel încât reactivitatea de scurgere creată de această inductanță să fie o valoare specifică la frecvența de funcționare dorită. În acest caz, parametrul real de funcționare util nu este valoarea inductanței de scurgere, ci valoarea inductanței la scurtcircuit. .
Transformatoarele comerciale și de distribuție cu putere de până la 2500 kVA sunt proiectate de obicei cu impedanțe de scurtcircuit între 3% și 6% și cu raportul X/R (rezistență la înfășurare/rezistență la înfășurare) corespunzător între 3 și 6, care definește modificarea procentuală a tensiunea secundară între sarcina goală și cea completă. Astfel, pentru sarcini pur rezistive, reglarea tensiunii complete și goale a acestor transformatoare va fi între aproximativ 1% și 2%.
Pentru unele aplicații de rezistență negativă, cum ar fi semnele de neon, unde este necesară amplificarea tensiunii (funcționarea transformatorului), precum și limitarea curentului, sunt utilizate transformatoare de înaltă tensiune de înaltă tensiune. În acest caz, rezistența la scurgere este de obicei de 100% din impedanța de încărcare completă, deci chiar dacă transformatorul este rupt, nu va fi deteriorat. Fără inductanță de scurgere, rezistența negativă caracteristică a acestor lămpi cu descărcare le va determina să conducă un curent excesiv și să distrugă.
Transformatoarele cu inducție de scurgere variabilă sunt utilizate pentru a controla curentul în mașinile de sudat. În aceste cazuri, inductanța de scurgere limitează curentul la valoarea dorită.
Reactivitatea scurgerii transformatorului joacă un rol major în limitarea curentului de defect al circuitului în cadrul valorii maxime admise în sistemul de alimentare. [2]
- Cum să alegi cizmele în funcție de silueta ta Verifică ce model este potrivit pentru tine! Blog
- Spuneți NU steroizilor! Alege viața!
- Cum se alege un ceas cu alarmă How2bg
- Cum să alegeți ierburi pentru nevroza fricii și pastile
- Cum să alegeți o mașină pentru tractarea unei rulote - Portalul bulgar de camping și caravaning