Ecuația radar
Ecuația radar într-o formă simplă și vizuală conectează intervalul maxim al radarului, parametrii acestuia și parametrii țintă. În funcție de rezultatul dorit, ecuația radar poate fi scrisă în raport cu domeniul maxim al radarului sau cu puterea undei electromagnetice la intrarea antenei de recepție. În al doilea caz, puterea Pe a antenei radar receptoare este exprimată în funcție de puterea radiată PS, domeniul țintei R și caracteristicile de reflectanță ale țintei descrise de suprafața sa efectivă de împrăștiere σ. Dacă se cunoaște sensibilitatea receptorului radar, atunci ecuația radar poate fi utilizată pentru a determina domeniul maxim de radar teoretic realizabil. Astfel, ecuația radar poate fi utilizată pentru a estima performanța radarului.
Derivarea ecuației radar
La început, să presupunem că propagarea undelor radio are loc în condiții ideale, adică fără pierderi.
Figura 1. Densitatea de putere emisă de un radiator omnidirecțional scade odată cu expansiunea geometrică a fasciculului (cu distanța față de radiator)
Figura 1. Densitatea de putere emisă de un radiator omnidirecțional scade odată cu expansiunea geometrică a fasciculului (cu distanța față de radiator)
Dacă energia de înaltă frecvență este emisă de un radiator izotrop sferic, atunci este distribuită uniform în toate direcțiile. Prin urmare, suprafețele cu aceeași densitate de putere sunt sfere a căror zonă, în funcție de distanța de la radiator, este definită ca (A = 4 π R²). Aceeași cantitate de energie cu raza crescândă a sferei este distribuită pe o zonă în creștere a suprafeței sale. Aceasta înseamnă că densitatea puterii undei electromagnetice de pe suprafața unei sfere este invers proporțională cu pătratul razei sferei. În acest fel, se poate scrie o ecuație pentru a calcula densitatea de putere Su emisă de un radiator izotrop:
- PS - putere radiată [W]
- R1 - distanța de la antena de transmisie la țintă [m]
Figura 2: Amplificarea antenei prin densitatea puterii oferă densitatea puterii direcționale.
Figura 2: Amplificarea antenei prin densitatea puterii oferă densitatea puterii direcționale.
Dacă antena de transmisie este îndreptată, aceasta duce la o creștere a densității de putere emise într-o anumită direcție. Acest efect se numește amplificare a antenei. În acest fel, expresia pentru densitatea de putere a radiatorului direcțional Sg poate fi scrisă în formă
Desigur, antenele radar nu emit cu adevărat emițătoare izotrope „parțial emitente”. Antenele radar trebuie să aibă o lățime mică a fasciculului și un câștig de 30 sau 40 dB (de exemplu, o antenă parabolică reflectorizantă sau o antenă cu matrice fazată).
Detectarea țintei depinde nu numai de densitatea de putere din zona țintă, ci și de cât de multă din această putere se reflectă în direcția radarului. Pentru a determina puterea efectivă reflectată, este necesar să se cunoască suprafața efectivă de împrăștiere σ a țintei. Valoarea sa depinde de mulți factori, dar se poate argumenta că o țintă cu o suprafață mai mare reflectă mai multă putere decât o țintă cu o zonă mai mică. Aceasta înseamnă că, în aceleași condiții de observare, o aeronavă de pasageri are o zonă de împrăștiere mai mare decât o aeronavă sportivă.
Rezultă din cele de mai sus că puterea reflectată Pr a țintei depinde de densitatea puterii Su, de câștigul antenei G și de suprafața de împrăștiere efectivă în schimbare σ:
Într-o formă simplificată, ținta poate fi considerată ca un emițător. În această abordare, puterea reflectată Pr este considerată puterea radiată.
Aplicând același argument puterii reflectate ca și puterii radiate, prin analogie cu formula (1), putem scrie expresia densității puterii Se a antenei de recepție:
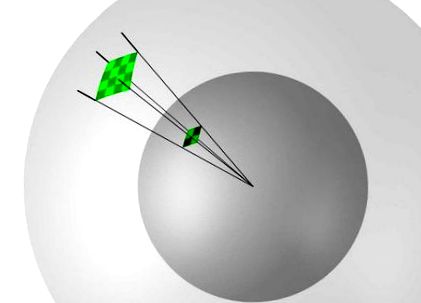
Figura 3. Relația dintre expresiile (3) și (4)
- R2 - distanța dintre țintă și antena de recepție.
Figura 3. Relația dintre expresiile (3) și (4)
Puterea obținută Pe a antenei de recepție depinde de densitatea puterii în poziția de recepție Se și de aria efectivă a antenei AW .
Evident, valoarea zonei efective a antenei caracterizează partea de putere pe care antena o poate „colecta” din fluxul total de putere reflectat de țintă. Cu cât suprafața antenei este mai mare, cu atât poate „colecta” mai multă energie pentru ea însăși. În plus, acest parametru se datorează prezenței pierderilor de antenă. Din acest motiv, puterea primită de la antenă nu este egală cu puterea care cade pe ea. Eficiența antenei este descrisă cantitativ, utilizând factorul de eficiență Ka, a cărui valoare pentru antenele reale este de obicei de aproximativ 0,6 ... 0,7.
Factorul de eficiență al antenei conectează aria sa geometrică și efectivă, adică.
Luând în considerare valorile introduse, expresia pentru puterea obținută Pe poate fi scrisă astfel: Ținând cont de valorile introduse, expresia puterii primite Pe poate fi scrisă sub forma:
În expresiile de mai sus, undele emise și reflectate sunt considerate separat. Următorul pas este de a obține o expresie care să le conecteze parametrii. Prin urmare, înlocuim expresia pentru puterea reflectată (3) în formula pentru puterea obținută (8). În continuare vom lua în considerare faptul că pentru cazul unui radar monostatic R1 = R2 .
Câștigul antenei G poate fi exprimat prin lungimea de undă λ. Fără a deduce concluzia acestei expresii aici, scriem formula finală:
Exprimând din (10) aria geometrică a antenei A și înlocuind expresia obținută în (9), după simplificare obținem:
Rezolvând ecuația rezultată pentru domeniul țintă R, obținem ecuația clasică pentru domeniul radarului:
Ecuația rezultată ia în considerare toate cantitățile care afectează propagarea semnalelor radar. Înainte de a încerca să puneți în practică ecuația radar, de exemplu, pentru a evalua eficacitatea radarului, sunt necesare câteva considerații suplimentare.
Pentru un radar dat, majoritatea parametrilor (în special Ps, G, λ) pot fi considerați constanți, deoarece valorile lor variază în limite mici. Pe de altă parte, suprafața efectivă de împrăștiere se schimbă destul de puternic. Cu toate acestea, în scopuri practice, se presupune adesea că este egal cu 1 m².
Cea mai mică putere recepționată la care poate fi detectat semnalul reflectat este PEmin. Semnalele cu putere mai mică decât PEmin nu pot fi utilizate, deoarece se vor pierde în zgomotul receptorului. Prin urmare, PEmin este numit și sensibilitatea receptorului. Valoarea PEmin determină intervalul maxim de radar Rmax:
Utilizarea acestei ecuații radar facilitează explicarea efectului unei anumite caracteristici radar asupra razei sale de acțiune.
Raportarea pierderilor
Derivația de mai sus a ecuației radar se face presupunând condiții ideale pentru propagarea undelor electromagnetice, adică. distribuție fără pierderi. De fapt, este necesar să se ia în considerare diverse pierderi, deoarece acestea pot afecta semnificativ eficiența radarului. În acest scop, ecuația radar este completată de factorul de pierdere Lges .
Acest factor ia în considerare următoarele pierderi:
- L D - pierderi interne în căile de transmisie și recepție ale radarului;
- L f - pierderea fluctuației în timpul reflectării țintei;
- L Atm - pierderi atmosferice - pierderi datorate absorbției undelor electromagnetice în timpul propagării lor în atmosferă de la radar la țintă și înapoi.
Pierderile interne apar și la componentele radarului de înaltă frecvență, cum ar fi ghidurile de undă, filtrele și carcasele antenei. Pentru un radar dat, aceste pierderi sunt relativ constante și pot fi ușor măsurate.
Atenuarea atmosferică și reflexiile de la suprafața pământului sunt factori constanți.
Autorul originalului german: Christian Wolf, Traducere în bulgară: Jeanne Wolf
Utilizarea acestui site și a conținutului acestuia este permisă în conformitate cu GNU Free Documentation License (GFDL).
și Creative Commons Attribution-Share Alike 3.0 pot avea termeni suplimentari.
- FUNDAMENTE FIZIOLOGICE DE NUTRIȚIE Lucrare din Biologie
- Dieta strictă elementele sale de bază, tipurile, regulile și meniul - Revista pentru femei
- Ecuații ale mecanicii mediilor continue
- S-a rezolvat! TVA la alimentele donate în țara noastră este eliminată
- Encefalopatie cronică traumatică